Why We Need New Metrics

In my last post, I’ve argued against the use of degree of regularity-based bounds for conservatively estimating the complexity of a Gröbner basis attack. In a nutshell, all these bounds are upper bounds, where we really need lower bounds.

For example, consider the polynomial system $\mathcal{F} = \{f_0, f_1, f_2\} \subseteq \mathbb{F}[x, y, z]$ for some finite field $\mathbb{F}$ with\[f_0 = x^{100}z + y, \qquad f_1 = x, \qquad f_2 = z \;.\] Independent of the monomial order, the reduced Gröbner basis of $\mathcal{F}$ is $\mathcal{G} = \{x, y, z\}$. The degree of regularity of $\mathcal{F}$ is $101 = \deg(f_0)$. The Macaulay bound for $\mathcal{F}$ is equal to the degree of regularity. Looking only at these numbers might give the impression that computing $\mathcal{G}$ is difficult. However, after constructing just one S-Polynomial $f_0 – x^{100} \cdot f_2 = y$, the Gröbner basis is already computed. All that’s left is reducing now redundant $f_0$, and we have the reduced Gröbner basis, $\mathcal{G}$.

Vectors of Origin – Explaining GBs

The connections between polynomials of some system $\mathcal{F}$ and its Gröbner basis $\mathcal{G}$ are usually not clear at all. For example, consider $$\mathcal{F} = (x^2 + z^2, z^2t + t, xy^2 + y + 1, x^2y + x)$$ and its reduced Gröbner basis $$\mathcal{G} = (x, y + 1, z^2, t).$$ Which input element was required for which Gröbner basis elements? Can some Gröbner basis elements be derived by using only a subset of the input? How were the input elements combined?

Vectors of origin (voo) answer these – and potentially more – questions. A voo $\mathbf{v} \in \mathbb{F}[x_0, \dots, x_{n-1}]^{|\mathcal{F}|}$ for some Gröbner basis element $g \in \mathcal{G}$ is a vector of polynomials such that $\mathcal{F} \cdot \mathbf{v} = g$. For example, $(0, 0, x, -y)$ is the voo for $x \in \mathcal{G}$. Arranging all voo’s into matrix $\mathcal{V}$, we have $\mathcal{F} \cdot \mathcal{V} = \mathcal{G}$. This $n\times |\mathcal{F}|$ matrix, where each entry is a multivariate polynomial, contains a lot of juicy information about $\mathcal{F}$.

We can compute voos by tweaking Gröbner basis algorithm F₅. F₅ uses signatures to avoid many useless reductions – and a signature is essentially derived from a voo, even though the voo is usually not computed explicitly. By modifying existing code for F₅ slightly, we can thus easily get $\mathcal{V}$ in addition to $\mathcal{G}$.

Involvement of the Input System

An element $g$ of a Gröbner basis is not necessarily the polynomially weighted sum of all input polynomials, as the examples above show. I have dreamed up a metric measuring how many elements of a reduced Gröbner basis rely on how many input system elements. Its working title is the ”involvement” metric. It’s not finished, but you might find the ideas interesting.

The involvement of some system $\mathcal{F}$ is the normalized measure of how many elements of $\mathcal{G}$ depend on how many polynomials in $\mathcal{F}$. More precisely, denote the number of non-zero entries in voo $\mathbf{v}_i$ by $v_i$. The mean of all $v_i$’s is the mean number of input elements making up the Gröbner basis elements. Since every Gröbner basis element is the combination of at least one input polynomial, we can safely subtract $1$ from $v_i$ before taking the mean, without losing information. This has the added benefit that the involvement metric is $0$ if the input is a Gröbner basis, since the vectors of origin will be (a subset of) the identity vectors. Normalizing this mean, i.e., dividing it by $|\mathcal{F}| – 1$ such that the result is in the interval $[0, 1]$, then gives the involvement metric. This sagemath one-liner below captures this description more concisely:

mean([sum([1 for v in voo if v])-1 for voo in V]) / (len(F)-1)

Let’s return to the example above. The matrix $\mathcal{V}$ with all vectors of origin is $$\mathcal{V} = \left(\begin{matrix} 0 & 0 & x & -y \\ 1 & 0 & -x^2 & xy \\ 0 & 0 & -xy^2+1 & y^3 \\ -xyt-t & xy+1 & -xyt & y^2t+xt \\ \end{matrix}\right).$$ We have $v_0 = v_2 = 2$, $v_1 = 3$, and $v_3 = 4$. The mean is $\frac{\sum v_i – 1}{4} = \frac{7}{4}$, normalizing (in this case) corresponds to a division by $3$, so the result is $\frac{7}{12} \approx 0.583$.

Involvement as Number of Non-Zero Coefficients

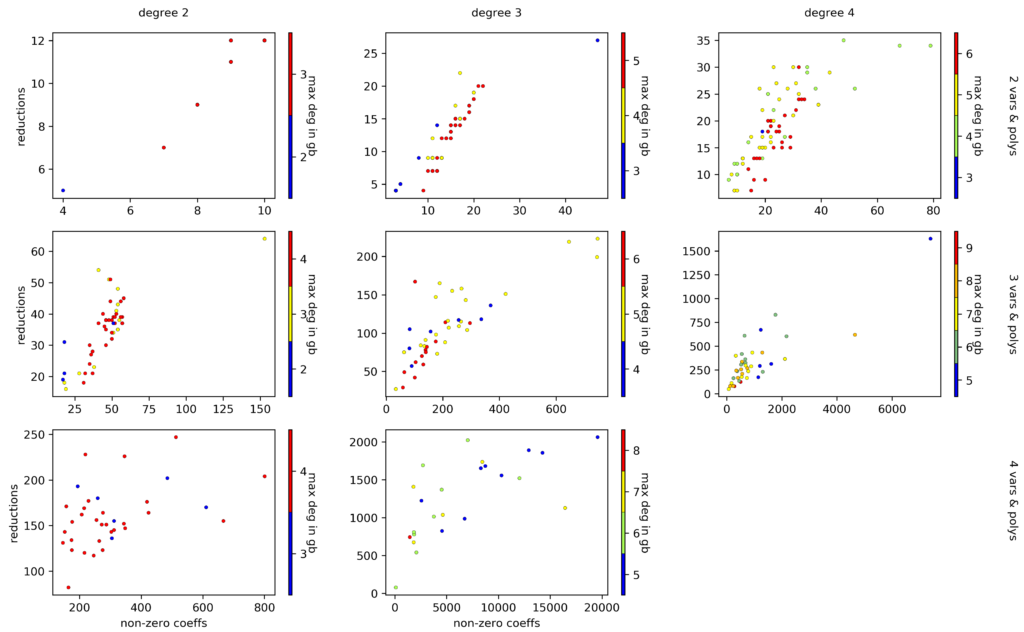
Simply counting the number of non-zero entries in a voo throws away quite a bunch of information. A different idea is to count the number of all non-zero coefficients in all the polynomials in $\mathcal{V}$. Continuing above example, that’d give a value of $15$. This approach might capture the complexity of computing a Gröbner basis more accurately, in part because large and involved $\mathcal{V}$s don’t just get squeezed into the interval $[0,1]$. The figure below suggests a correlation between the complexity of computing a Gröbner basis and the total number of non-zero coefficients in all voos, but it is still quite noisy.

Including the Degree of the Voos

It is tempting to somehow mix the degrees of the voos into the involvement metric. However, I have not yet found a good way to do so, partly because the degrees of the voos can be very large even for very easy Gröbner basis computations.

For example, take $\mathcal{F}_{10} = ( x^{10}y + 1, xy^{10} )$. The reduced Gröbner basis for $\mathcal{F}$ is $\{1\}$, i.e., $\langle \mathcal{F} \rangle = \mathbb{F}[x, y]$. However, the two polynomials in the single vector of origin are both of degree $99$, far bigger than the Macaulay bound, which is $21$. In total, $10$ reductions are required to find the reduced Gröbner basis.

For system $\mathcal{F}_{100} = ( x^{100}y + 1, xy^{100} )$, the reduced Gröbner basis is still $\{1\}$. The Macaulay bound has increased to $201$, but the degrees of the two polynomials in the vector of origin is now $9999$, even though only $100$ reductions were required to compute the reducer Gröbner basis!

The degrees of the polynomials in the voos might not be of any practical relevance – at least, I haven’t spotted one yet. The argument might even be irrelevant for polynomial systems derived from a cryptographic primitive, since above examples might only work because $1$ is in the ideal spanned by $\mathcal{F}_{10}$ and $\mathcal{F}_{100}$.

Conclusion

Above ideas are still rather rough and need to be developed quite a bit before they can be useful. Regardless, I believe they might be a step in the direction for developing a lower bound for the complexity of computing a Gröbner basis of a given polynomial system. Or if not that, then maybe a heuristic, another tool for primitive designers to argue resistance against Gröbner basis attacks.