Have you ever computed a Gröbner basis in some monomial order ≺₀ only to then realize that you actually wanted it in another order ≺₁? I know, happens all the time… But fret not, FGLM can convert between the two orders, and you don’t have to start your computation from scratch.

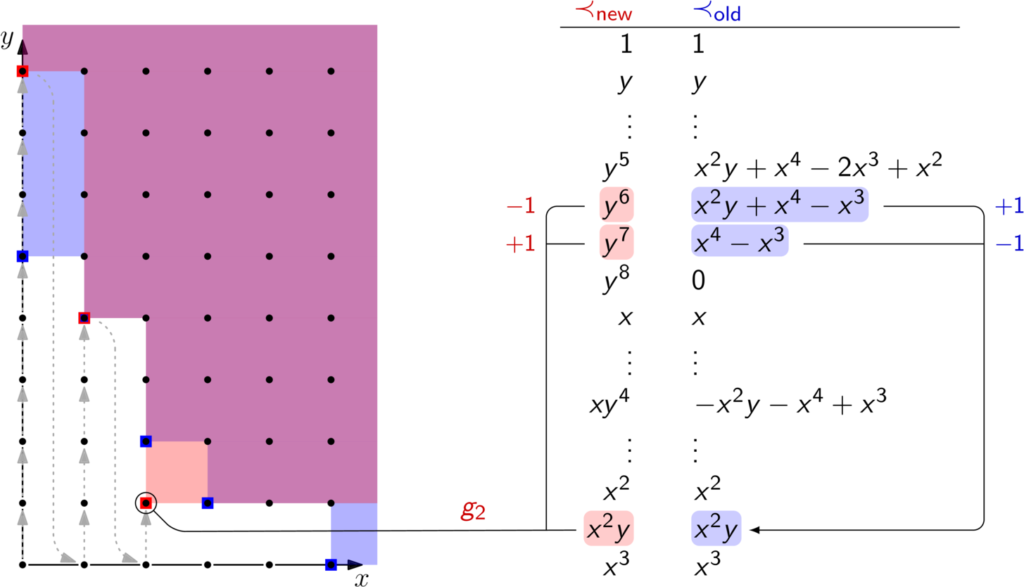
Here’s a recording where I’m explaining how FGLM works. If you’d like to look through the slides at your own pace, here they are. You can also find the two Gröbner bases used in the example as well as pseudocode for FGLM in the slides, in case you want to retrace the steps yourself.

If you are interested in not only how but also why FGLM works, have a look at the original publication. Section 5 and 6 give a comprehensive overview of FGLM’s complexity, which can be summarized as O(n·D³) where D is the dimension of quotient ring k[x₀, …, x_n-1] / <G> as a k-vector-space. More intuitively, D is the number of monomials in the staircase of a Gröbner basis, which are those dots in the non-blue region in this post’s first picture.

Next Wednesday, 12 August 2020 at 16:30 CET, our own Ferdinand Sauer will be giving an introductory presentation on Gröbner basis attacks in the context of attacking arithmetization-oriented ciphers. Be sure to tune in if you want to learn more about the attack space for AO ciphers like Rescue and Poseidon. Email us if you want access to the zoom link.

Update: Slides & VoD

Couldn’t make it? Not to worry! Take a peek at the slides, and complement them by watching the recording.

Researchers at StarkWare have published a report detailing their decision process of hash function for hashing over STARKs. In the end they chose for the arithmetization oriented cipher Rescue. The report also includes an appendix by Jean-Charles Faugère and Ludovic Perret about the security of these ciphers against Gröbner basis attacks. Read the report here.